11865. Baku Metro
The Baku Metro is one of the oldest and
most unique in the region. The first line was opened in 1967, and today
the network includes dozens of stations, such as “28 May”, “Icheri Sheher”, “Nizami”,
and others. One of the distinctive features of the Baku metro is its deep,
mosaic-decorated stations and the presence of transfer hubs. In recent years,
there has been an active discussion about the construction of a circular line
that would connect central and peripheral areas of the city.
As part of the capital's metro
modernization project, an abstract model of the metro network was developed,
consisting of n stations and n tunnels
between them. Each tunnel connects exactly two stations and does not intersect
any others. Moreover, it is possible to travel from any station to any other by
moving along the tunnels. All tunnels are bidirectional, and there is at most
one direct connection between any pair of stations.
Mathematicians in Baku have proven a
theorem: in any such metro scheme, there exists exactly one cycle. In other
words, a circular line can be found – a route passing through several stations,
where any two neighboring stations are connected by a tunnel, and no station
appears more than once.
This discovery caused a real sensation in
the city: residents began to compare the distances of their stations to the
circular line. One might say: “I live three stations from the circle”, while
another boasts, “Only one for me.” Mobile apps even appeared to calculate the
distance of a station from the ring line (with a paid subscription, of course).
To take control of the situation, the Baku
Metro Administration tasked you with developing a program that, given a map of
the metro network, calculates for each station the minimum number of stations
needed to reach the circular line. For stations on the circular line, the
distance is considered to be zero.
Input. The first line contains an integer n (3 ≤
n ≤ 3000) – the number of stations in the metro network (which
also equals the number of tunnels). The next n lines each describe one
tunnel. Each line contains a pair of integers xi, yi
(1 ≤ xi, yi ≤ n),
indicating a tunnel between stations xi and yi.
Stations are numbered
from 1 to n in arbitrary order.
It is guaranteed that xi
≠ yi, there is at most one tunnel between any
pair of stations, and all tunnels are bidirectional. It is also guaranteed that
the given metro map is classical – that is, connected and contains exactly one
cycle.
Output. Print n integers: the i-th
number should represent the distance from the i-th station to the
circular line. For stations that are on the circular line, print 0.
|
Sample input 1 |
Sample output 1 |
|
5 1 2 1 4 5 3 5 2 3 4 |
0 0 0 0 0 |
|
|
|
|
Sample input 2 |
Sample output
2 |
|
6 1 2 2 3 2 5 3 5 3 4 6 4 |
1 0 0 1 0 2 |
SOLUTION
breadth first search
Algorithm analysis
A connected
undirected graph with n vertices and n edges is given. The graph
contains exactly one cycle. For each vertex, it is required to determine the
shortest distance to the nearest vertex that lies on the cycle. If the vertex
itself is part of the cycle, the distance is considered to be 0.
The graph can be
thought of as a single cycle with tree-like branches (i.e., acyclic subgraphs)
attached to it. To identify the vertices that belong to the cycle, we use a
leaf removal process (removing vertices of degree 1 step by step):
·
While there are vertices of degree 1 in the graph, remove
them.
·
When no such vertices remain, the remaining vertices form the
cycle.
This process
resembles a reverse topological sort: we iteratively remove the leaves until
only the “inner” vertices remain – these are
precisely the ones that make up the cycle.
Next, perform a
breadth-first search starting simultaneously from all vertices of the cycle. In
this way, for each remaining vertex, we compute the minimum number of steps
(transitions) needed to reach the nearest vertex on the cycle.
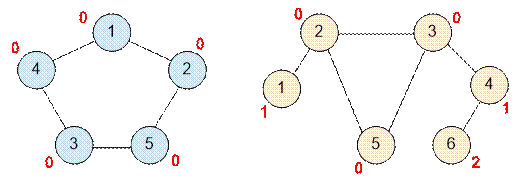
Example
In the first example, all
vertices are part of a single cycle, so the distance for each of them is 0.
In the second example, the
cycle consists of vertices 2, 3, and 5, while the remaining vertices are
located at some distance from it.
Algorithm implementation
Declare the adjacency list g for the graph, as well as the
following auxiliary arrays:
·
used – stores the state of each vertex (whether it has been
removed or is part of the cycle);
·
dist – stores the distance from each vertex to the nearest vertex
that lies on the cycle;
·
deg – stores the degree of each vertex (i.e., the number of
adjacent vertices).
vector<vector<int> > g;
vector<int> used, dist, deg;
queue<int> q;
Read the input data and construct the graph.
scanf("%d", &n);
g.resize(n
+ 1);
for (i = 0; i < n; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Compute the degree of each vertex. Vertices with degree 1 are added to the
queue q.
used.resize(n
+ 1, 0);
deg.resize(n
+ 1, 0);
for (i = 1; i <= n; i++)
{
deg[i] = g[i].size();
if (deg[i] == 1)
{
q.push(i);
used[i] = 1;
}
}
Next, perform a breadth-first search, starting simultaneously from all
vertices of degree 1. During the traversal, the vertices that do not belong to
the cycle will be marked as visited – they are gradually “pruned” from the
graph like leaves.
while (!q.empty())
{
int v = q.front(); q.pop();
for (int to : g[v])
if (used[to] == 0)
{
deg[to]--;
The BFS continues from a vertex to only if its degree becomes equal
to 1 – meaning it has turned into a new leaf.
if (deg[to] == 1)
{
q.push(to);
used[to] = 1;
}
}
}
At this point, the value used[i] = 0 only if vertex i
belongs to the cycle. Now we add all cycle vertices to the queue q. We
also initialize the dist array, which will store the shortest distances
from each vertex to the nearest vertex on the cycle.
dist = vector<int>(n + 1, -1);
q = queue<int>();
for (i = 1; i <= n; i++)
if (used[i] == 0)
{
q.push(i);
dist[i] = 0;
}
Perform a breadth-first search, starting from the vertices already in the
queue q – these are the vertices that belong to the cycle. During the
traversal, compute the distances from the cycle to all other vertices in the
graph.
while (!q.empty())
{
int v = q.front(); q.pop();
for (int to : g[v])
if (dist[to] == -1)
{
q.push(to);
dist[to] = dist[v] + 1;
}
}
Print the answer.
for (i = 1; i <= n; i++)
printf("%d ", dist[i]);
printf("\n");